Demystifying the concept of pKa
- Benjamin Hui
- Feb 12, 2019
- 4 min read
Updated: Feb 13, 2019
Earlier, we discussed the concept of chemical equilibrium, and why all reactions can be considered to be in equilibrium between products and reactants. We also discussed that the equilibrium constant, K(eq), is the ratio of products to reactants and its positive, negative or zero values determine the spontaneity of the reaction.
Now we will apply this concept to a special class of compounds which we should be familiar with: acids, or more specifically, Brönsted acids. These compounds only have a singular purpose in their existence, and that is to release a proton, or two, or three, depending on how many they have. Because of this completely specific reactivity, the equilibrium constant of the proton release reaction is given a unique name: the acid dissociation constant, K(a) and is represented by the general equation:
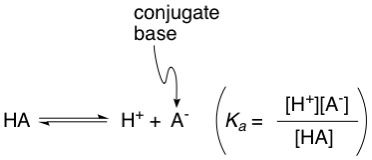
As with K(eq), the larger the K(a), the more products there are, meaning more protons (H+) and conjugate base (A-). And since acid strength depends on the amount of H+ (more H+ = stronger acid), the larger the K(a), the stronger the acid. Now some acids are so strong that K(a) is super large, and some acids are so weak that K(a) is super small, so it's not practical to quote these numbers every time we talk about these acids, therefore, chemists decided to take the negative base 10 logarithm of K(a), making the numbers much easier to work with. We now have a new term called pK(a), or simply pKa.
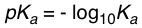
Because of the negative sign in the formula, we find that the lower the pKa, the stronger the acid i.e. the more it wants to give away its proton, and the less the resultant conjugate base wants it back. Conversely, the higher the pKa, the weaker the acid i.e. the less it wants to give away its proton, and the more the resultant conjugate base wants to hold on to it. Therefore, we can actually use pKa values to assess both acid strength and base strength, and predict if a particular acid can be deprotonated by a particular base, or put another way, if a particular base can be protonated by a particular acid. Both these phrases are interchangeable because they mean essentially the same thing.
To demonstrate this, let's bring up a pretty decently populated pKa list containing several acids with their corresponding conjugate bases:
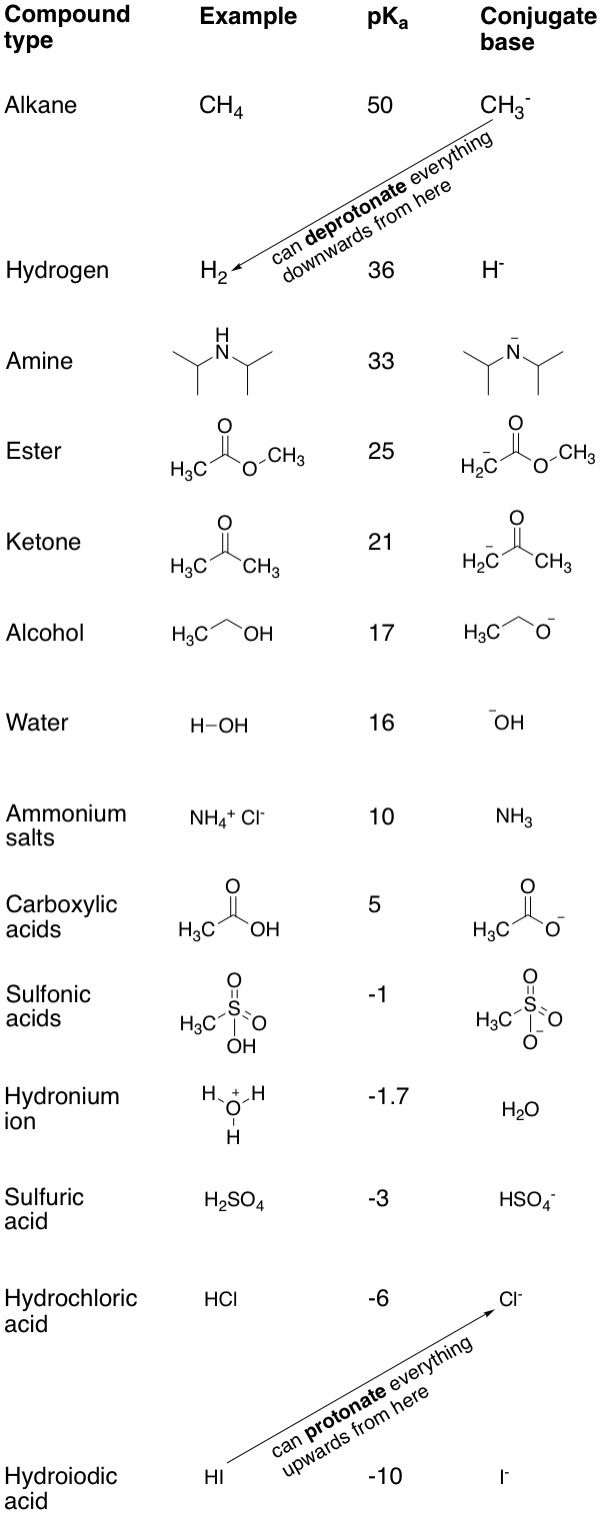
At the top of the list are the alkanes, which we usually don't associate with being acids, and we'd be quite right: alkane hydrogens are hardly acidic and never want to leave. The pKa of 50 reflects this. You can't get more non-acidic than that. This means that if we were able to obtain the conjugate bases of alkanes (and we can, in the form of commercially available alkyllithium reagents e.g. n-butyllithium), they would be the strongest bases ever known and would rip protons off pretty much any other type of compound to become alkanes again. Hence we see that the conjugate base of methane, the methyl anion, is able to pull a proton off any compound below and including hydrogen. In other words, if acid A (e.g. methane) has a higher pKa than acid B (e.g. hydrogen), then acid A's conjugate base (methyl anion) would be able to deprotonate acid B (hydrogen). The equilibrium would then be in favour of the right side of the equation

If we started from the bottom of the list, it would be the same idea, just from a different perspective. The pKa of hydroiodic acid is very low at -10, meaning it's a super strong acid. Its proton is a loose cannon and would prefer to be anywhere else but with iodide (I-). This also means that iodide is such a weak base that it wouldn't be able to grab a proton from anywhere at all. Therefore, we see that HI is able to donate its proton to any base above and including Cl-. In other words, if acid A (e.g. hydroiodic acid) has a lower pka than acid B (e.g. hydrochloric acid), then acid A would be able to protonate the conjugate base of acid B (Cl-). The equilibrium would then be said to favour the right side of the equation

If you said that Cl- deprotonates HI, since HCl has a higher pKa than HI, you would be entirely correct as well. We can see that both of the above statements about protonation or deprotonation are essentially identical, if made from a pKa perspective.
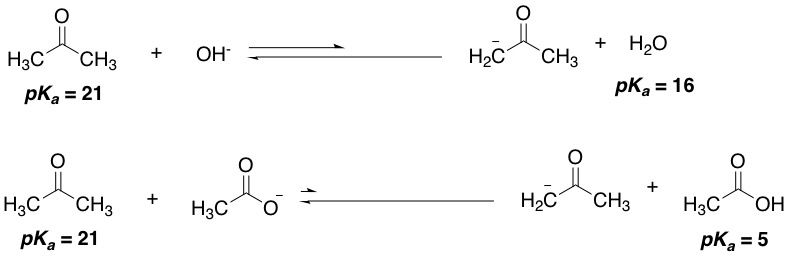
In the lab, if a chemist wanted to deprotonate a particular compound, the general rule of thumb is to pick a base whose corresponding conjugate acid's pKa is at least 5 units greater. For example, if we wanted to deprotonate a ketone (pKa = 21), we would use an amide base, since their conjugate acids, amines, have pKas of around 33. The reason behind this is to push the equilibrium almost fully towards products. If we used a base only 1 or 2 pKa units greater, say an ester enolate, then the reverse reaction would relatively have a much greater chance of occurring and we wouldn't get much products.
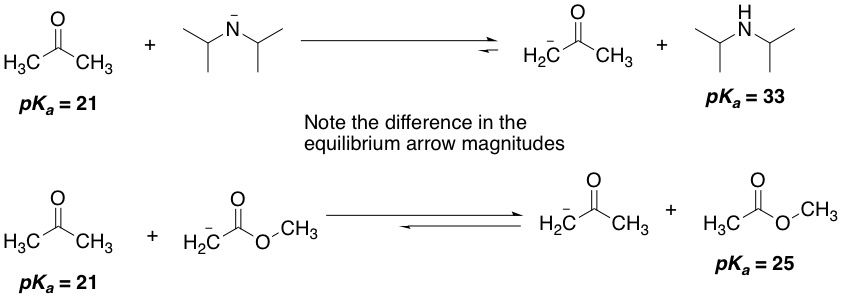
You may be thinking: Wait a minute. If the reverse reaction is taking place, doesn't that mean that a lower pKa compound is deprotonating a higher pKa one? I thought only higher pKas can deprotonate lower pKas! A good question, and the answer is yes, it does. What this means is that the deprotonation isn't as favourable now, and we will get an equilibrium favouring the reactants instead. Let's have an example, and we'll use hydroxide, the conjugate base of water (pKa = 16). To this we'll add some ketone (pKa = 21). The hydroxide, in contrast with amide, will now have a harder time deprotonating the ketone, and the equilibrium will lie towards reactants. If we used carboxylate, the conjugate base of carboxylic acids (pKa = 5), a much much weaker base, the equilibrium will lie even more towards reactants. We would hardly get any product. As organic chemists, that's not what we like to see. Our eternal struggle is with equilibria, and finding reaction conditions that will drive the direction of the equilibrium towards as much products as possible. And pKa is one of the most important tools we have at our disposal to achieve that!


Comments