Spectroscopy in organic chemistry (pt. 2)
- Benjamin Hui
- Apr 1, 2019
- 7 min read
Introduction to NMR spectroscopy
Nuclear Magnetic Resonance (NMR) spectroscopy is perhaps the most powerful tool that organic chemists have at their disposal. It is capable of revealing structural information about molecules in multiple ways, and has revolutionarized the entire field of chemistry since its introduction in the 1950s. The basis of this technique is that atomic nuclei have a property called spin, and for reasons that are beyond the scope of this article, those that have an odd number of protons and/or neutrons have a magnetic dipole moment and can be observed by NMR. We say that these nuclei are NMR-active. Common nuclei observed in NMR are hydrogen (1H), carbon-13 (13C), fluorine-19 (19F) and phosphorus-31 (31P).
Let's take some time to talk about the origin of a nucleus' dipole moment. Nuclear spin is in fact quite literal: Atomic nuclei are always in motion; spinning, rolling and tumbling in random directions. And because nuclei are electrically charged, their movement generates a magnetic field and hence the dipole moment. Therefore, atomic nuclei are like tiny bar magnets. However, because they spin and roll and tumble in all directions, their magnetic moments cancel out overall, and so there is no energy difference between any of the orientations that they can have i.e. they are degenerate.
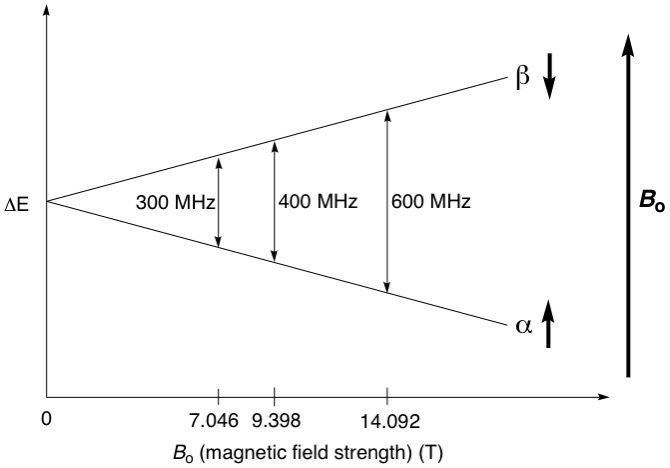
However, in the presence of an external, unidirectional magnetic field, the nuclei, since they are tiny bar magnets, will align themselves with the magnetic field, much like how a compass needle (nucleus) always aligns itself with the Earth's magnetic field (external magnetic field) to always point north. This is one of its spin states, called the alpha (α) spin state, and is the more energetically stable state, since it's aligned with the external field. Now, if we wanted our compass needle to point south, that would be impossible unless we forced it to by applying some energy to turn the needle 180 degrees. This is the other spin state, called the beta (β) spin state, and is the higher energy, unstable state (see diagram below). In the context of the hydrogen nucleus, or simply a proton (1H), which is a spin 1/2 nucleus, the α spin state is assigned the value of +1/2 and the β state is assigned -1/2.
So now that we have two different energy states, we can do NMR spectroscopy. It turns out that the energy difference between the α and β spin states corresponds to radio frequency (RF) wavelengths. So if we applied a quick pulse of RF energy to these protons corresponding to the energy difference, their spins would resonate i.e. "flip" from the α (where the majority of the nuclei originally were) to the β spin state. The excited nuclei will then gradually relax back to the α state by emitting RF energy that is picked up by a detector and converted into information. NMR spectrometers come with different operating magnetic field strengths. For example, a 400 MHz spectrometer provides a field strength of exactly 9.39798 teslas, which splits the α and β spin states of a proton to an energy difference of almost exactly 400 MHz (see diagram below). The stronger the magnetic field, the higher the energy difference between the α and β spin states, and the better the resolution of the resulting spectra. We will not be going into details about spectral resolution in this article.
Proton NMR analysis of organic molecules
Given the ubiquity of protons in organic molecules, proton NMR spectroscopy has become the de facto method for elucidating molecular structure. Now that we've established the basis of NMR, we can get into the nuts and bolts of obtaining a proton NMR spectrum, and interpreting it. There are several aspects of molecules that affect how their NMR spectra looks like, and we'll examine each of these closely.
1. Chemical equivalence
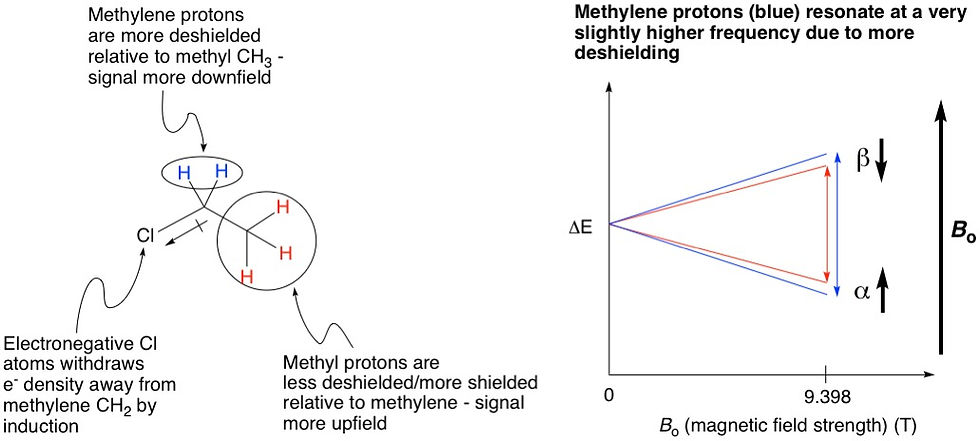
Groups of protons located in different parts of the molecule are in different electronic environments (due to proximity to electron-withdrawing or donating groups), and hence resonate at slightly different frequencies, for example, one group might resonate at 400.0001 MHz and another somewhere else would resonate at 400.0002 MHz.
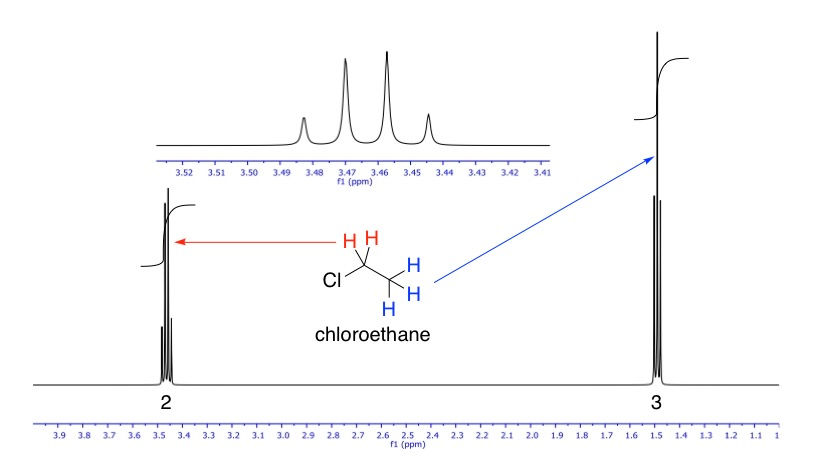
Let's look at an example, chloroethane. This molecule has two sets of protons, one as a methyl group (CH3), and the other as a methylene (CH2). The three protons at the methyl are all equivalent, because they are bonded to the same carbon. Similarly, the two protons at the methylene are equivalent because they are connected to the same carbon. The methyl group will hence show one signal, and the methylene will show another. So in total there will be two signals on the NMR spectrum. However, these two signals show up at different locations of the spectrum because these two groups of protons are in different electronic environments: the methylene group is closer in proximity to the chlorine, an electronegative atom that withdraws electron density from the vicinity of the methylene more than that of the methyl. Therefore, we say that the methylene is more deshielded than the methyl group. Because of this, the methylene protons are more exposed to the external magnetic field, leading to the α and β spin states being split very slightly more than methyl, leading to a slightly higher resonance frequency. This effect shows up on the NMR spectrum as the signal being located further downfield than that of the methyl (more on this below).
Now, as we know, chemists don't like working with big, cumbersome numbers like 400.0001 x 10^6 or 400.0002 x 10^6 Hz. So, we use a reference compound, which is almost universally tetramethylsilane Si(CH3)4, or TMS. All solvents used for NMR are doped with a tiny amount of TMS, so that when the sample is scanned, the spectrometer also locates the TMS signal and calibrates the spectrum accordingly. All the sample proton signals are then reported relative to TMS as....
2. ....Chemical shift
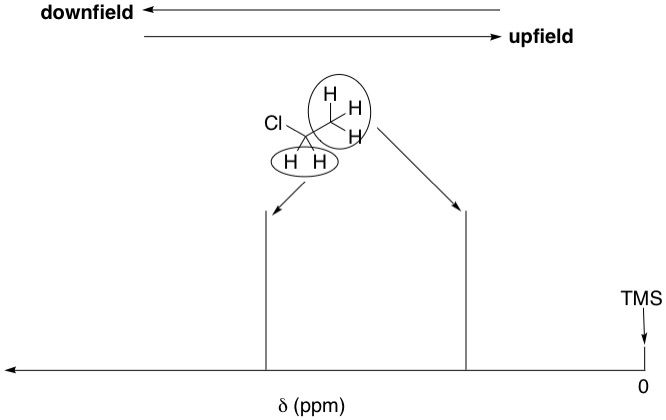
TMS is a symmetrical molecule. All of its methyl groups are equivalent because they are related by the tetrahedral angle of 109.5º. Therefore, TMS has only one signal, called a singlet, which is assigned as zero on the chemical shift (δ) scale, which is the x-axis of all NMR spectra. Zero on this scale starts at the far right of the spectrum (NMR spectra are read right-to-left: the further left, the more downfield, and the further right, the more upfield). All protons in the sample are reported relative to zero in terms of parts-per-million (ppm), called the chemical shift.
As we've just discussed, the methylene protons in chloroethane, being more deshielded, is shifted downfield relative to the methyl protons. Therefore, just by looking at the chemical shifts alone, we can deduce which signal belongs to which set of protons; the methyl or methylene.
3. Signal splitting (multiplicity)
The above "spectrum" hardly looks like an actual one. NMR signals are a lot more than simple straight lines. We have established that the protons in the methyl group are not equivalent with those in the methylene group, and vice versa. Since they are just adjacent to each other, their spins will interact in a process called coupling, and when they do, each of their signals will be split by the other into an (n + 1) pattern of peaks, where n is the number of protons in the neighbouring group. This is called a signal's multiplicity. For example, since the methyl group's neighbour is methylene, which has two protons, its signal will be split into 2 + 1 = 3 peaks i.e. a triplet. So its multiplicity is 3. Methylene's neighbour is methyl, which has three protons, therefore its signal will be split into 3 + 1 = 4 peaks i.e. a quartet. So its multiplicity is 4. The relative intensities of the peaks follow Pascal's triangle, where a triplet is always 1:2:1 and a quartet 1:3:3:1. The actual NMR spectrum of chloroethane is shown below.
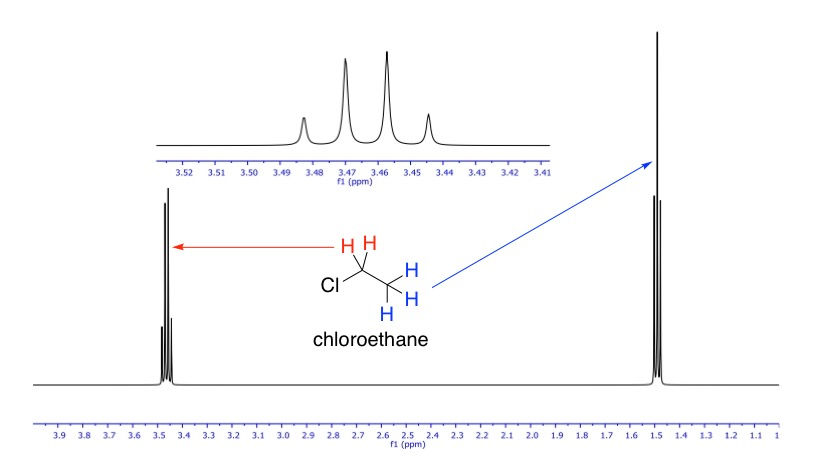
We can basically see in this spectrum everything that we've talked about so far: chemical shifts and signal splitting in the typical intensity ratios. The inset is a zoom-in of the quartet.
4. Integration
So now that we have a nice looking spectrum, can the spectrometer tell us how many protons there are in a signal? Well, the spectrum that we see is the result of post-mathematical processing called a Fourier Transform, automatically done by the computer (we don't need to know what it is). This makes it possible to calculate the number of protons in a signal by measuring the area under the peak. This is called integration. Nowadays this is all done by computer, but back in the day, spectra were printed out on graphing paper and chemists had to determine peak areas by hand.
However, integration cannot tell us the absolute number of protons in a signal. It is relative, so first of all, we need to know at least what one signal is and how many protons it contains, so that we can calibrate that signal, and the computer will do the rest by integrating the other signals relative to the calibrated signal.
Again looking at chloroethane, say we didn't know how many protons there are in the methyl signal, but we know how many the methylene signal has (2), we would tell the computer that that area corresponds to two protons. Once that's locked in, when we integrate the methyl signal, it should give us a value of 3. The complete NMR spectrum of chloroethane, with integrations, is shown below.
Special situations in NMR
Proton exchange:
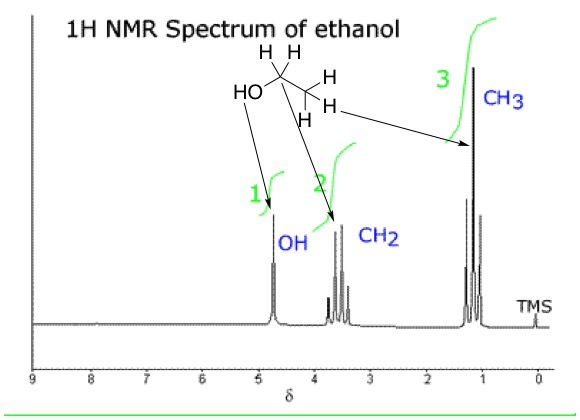
We know that bonds between hydrogen and electronegative atoms, say oxygen, are polarized because the electronegative atom pulls electron density from the bond towards itself. Polarized bonds are weaker than non-polarized ones, and so we say that these protons are "loose" or labile. Alcohols are a good example of this. Let's replace the chlorine in chloroethane with a hydroxyl group, giving us our familiar friend, ethanol. We would expect the NMR spectrum of ethanol to be different, because the methylene group would now have four neighbours (three from the methyl, one from hydroxyl) and should therefore have a signal split into a pentet (4 + 1 = 5). Methyl would still be a triplet because it still only has methylene as a neighbour. The hydroxyl proton would be a triplet because it has the two neighbours from methylene (2 + 1 = 3).
But as it turns out, the spectrum of ethanol isn't that much different than chloroethane, except for an extra singlet from the hydroxyl proton at a chemical shift of around 4.8 ppm. So this means that the methylene protons aren't coupling with the hydroxyl proton, and vice versa. What's going on here? Since the hydroxyl proton is labile, it is constantly exchanging with the proton from another molecule. The rate of this exchange is extremely fast, therefore the protons aren't in one place long enough to couple with the methylene protons. No coupling means no splitting, and so the hydroxyl proton remains as a singlet and the methylene remains a quartet.
With this, we conclude our series on spectroscopy. It is my hope that these articles will serve as an informative primer for this topic, and I strongly encourage consultation of online texts such as ChemLibre, or my personal favourite textbook: Introduction to Spectroscopy (any edition) by Pavia, Lampman, Kriz and Vyvyan which has helped me countless times not only during my time as a student, but as a PhD candidate and postdoc doing research.




Comments