The Power of Neighbouring Groups
- Benjamin Hui
- Dec 20, 2020
- 5 min read
By your second year, you would have come across a few substitution-type reactions of both the SN1 and SN2 mechanisms. In my experience, students seem to grasp SN2 reactions better because they are generally more straightforward: Nucleophile replaces the leaving group directly, and if there is stereochemistry to begin with i.e. solid wedge or dashed bonds, you simply flip it because the nature of the "backside attack" demands it (Figure 1). No need to worry about carbocations and the possibility of rearrangements.

Now, what if you were given a situation (Figure 2) where there are two separate SN2 reactions that look somewhat similar, but with very different rates and you were asked to explain why?
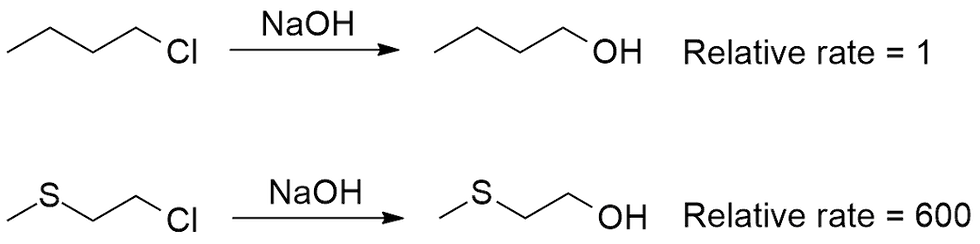
First thing to do is not panic, and look at the two starting compounds. There are no stereocenters, so you can safely not worry about that. Could it be sterics? The nucleophile (OH-) is constant, so it's not that. The electrophilic carbon atom containing the leaving group (Cl-) is also constant: a primary carbon, so we can also rule that out. Now your thought process should go: Okay, the only difference is that a sulfur atom has replaced one of the carbons in the chain, so obviously it has something to do with the sulfur. What does sulfur have that carbon doesn't? Thinking about it for a moment, you might recall that sulfur, like oxygen, usually contains a couple of lone pairs of electrons. The very nature of nucleophiles comes from them having lone pairs, so could sulfur here behave as a nucleophile? If you arrived at this conclusion, you would be absolutely right!
The next question to ask is, how does the sulfur act as the nucleophile here? There are two possible pathways: The first, an intermolecular one, involves one of the molecules attacking another in an SN2 process to form a sulfonium (S+) intermediate that is twice as large (and heavy) (Figure 3).
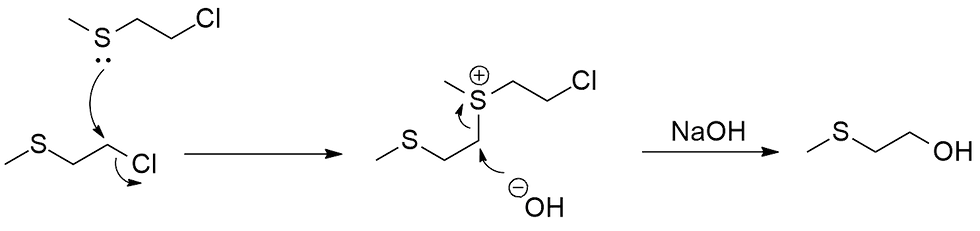
Notice that I said twice as large and heavy. What then does that tell us about the probability of this pathway? I would say unlikely, and this pathway would not give us the rate acceleration as we observed. Why though? Think about it, Cl- is already not a very good leaving group compared to the larger halides like Br- and I-. So, if you had another substrate molecule, which is way more cumbersome and sluggish than an OH-, approach and have to twist itself into the right orientation to attack, what would be the point of that? If anything it would just slow down the reaction even further. In fact it would be even faster if we just skipped the intermediate altogether and have the OH- directly attack instead to give the product right away; it's so much smaller, being essentially a rod and so has no need to twist itself about, and has a negative charge.
So the intermolecular pathway doesn't occur. What about an intramolecular one? This would be way more advantageous, since the nucleophile is already pre-installed: there is no need for the nucleophile to "find" the electrophile. This SN2 attack can occur pretty much right away, much faster than the OH- can attack, to generate a 3-membered sulfonium ring intermediate (Figure 4).
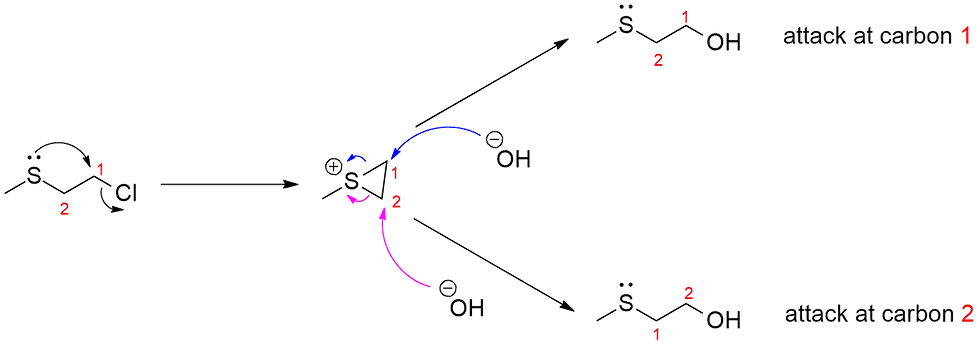
As you may know, 3-membered rings are inherently unstable because of severe torsional and angular strain, and now with a positively charged sulfur, this strongly polarizes the sulfur-carbon bonds, making them even weaker. The OH- is now very happy to attack this intermediate almost instantaneously in an SN2 fashion i.e. the fast step, and it has a choice: It could attack either one of the ring carbons (labelled red 1 and 2) to open the ring up and give the product. Notice that the same product forms regardless which carbon is attacked because of the lack of further substituent groups on those carbons, Of course, if there was further substitution on those carbons, then you must be very careful to keep track of them. I constantly emphasize numbering the carbons, especially when rings are involved so students can keep track of them.
So the overall effect of this intramolecular process greatly accelerates the nucleophilic substitution of Cl with OH via what is called neighbouring group participation (NGP).
Now let's look at another example, this one involving some stereochemical aspects. Say you were given the following two SN2 reactions, and the stereochemistry is inverted for one, and retained for the other (Figure 5).
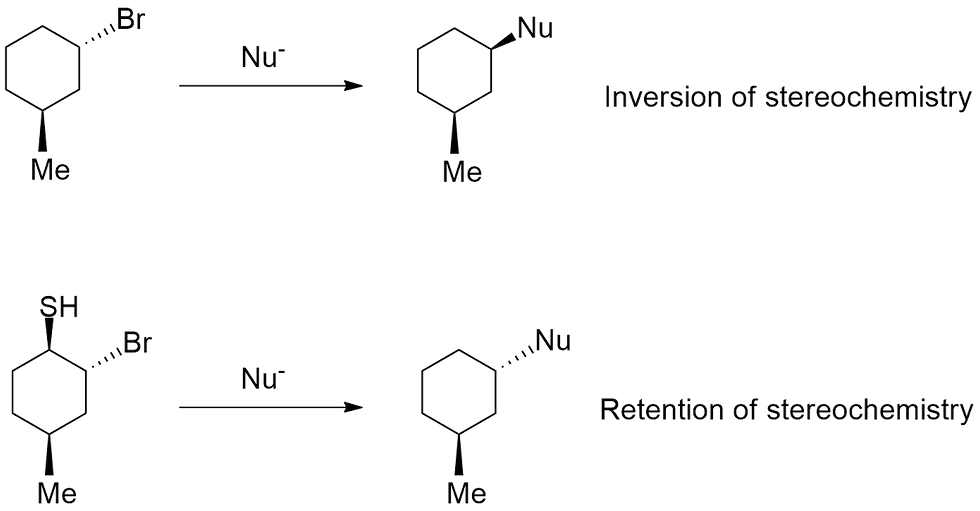
Again, you should ask yourself what the difference is between the two starting compounds? The bottom one contains an extra thiol (SH) group which then leads to a retention of stereochemistry when the nucleophile (Nu-) is introduced. From what you know about SN2 reactions, they should always lead to an inversion of stereochemistry i.e. a solid wedge becomes a dashed, and vice versa, because of the nature of the backside attack. The top reaction without the SH group reflects this fact.
Now that we've talked quite a bit about NGP, obviously the bottom reaction would involve that. Again, an intramolecular SN2 attack by a lone pair on the sulfur occurs first, to give a 3-membered ring intermediate. This gives a first inversion of stereochemistry at carbon 1. Now, we need to be careful when representing the stereochemistry of this ring. The starting SH group was a solid wedge (sticking out of plane towards you), and therefore the ring must also be sticking out of plane towards you. It is impossible for a 3-membered ring of this sort (attached to a larger structure) to have a solid wedge and a dashed wedge at the same time; it is geometrically impossible. Try building a model of that, and you might end up snapping one or more of the bonds. Now, once the 3-membered intermediate forms, the Nu- can now very quickly attack again at carbon 1 to give another inversion of stereochemistry and the final product. So the overall effect is a retention of stereochemistry at carbon 1 due to a sequential double inversion (Figure 6).

The anomeric effect
Let's switch gears now and talk about an effect of NGP on ring conformations, specifically, chair conformations of six-membered rings. We know that in general, substituents on these rings prefer to be equatorial to circumvent 1,3-diaxial interactions which are unfavourable. However, six-membered rings containing an oxygen atom i.e. pyranose are exceptional at a particular carbon atom in the ring, called the anomeric carbon. This is the atom right next to the oxygen. Substituents on this anomeric carbon tend to favour the axial position. In fact, a solution of D-glucose in water contains 64% of the axial form (alpha) and 36% of the equatorial form (beta) (Figure 7).
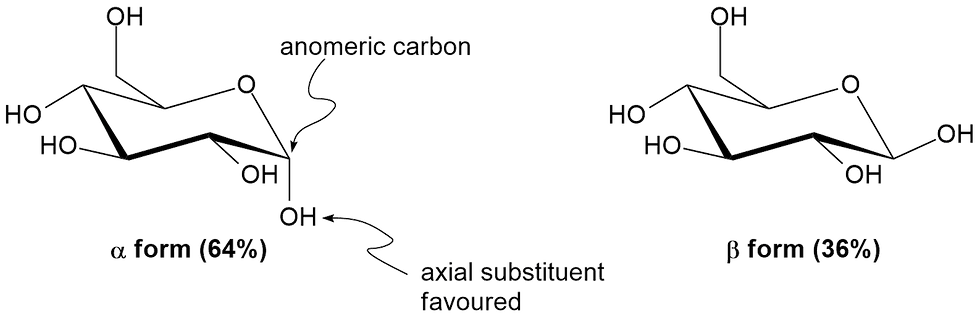
Let's investigate why by first appreciating the difference between this ring and a normal cyclohexane ring: a replacement of one of the ring carbons with an oxygen. Again, the reason has to be that oxygen atom contains lone pairs. Now, the orientations that these lone pairs adopt is the same as any substituent: one must be axial, and the other equatorial.
We're no longer talking about leaving groups, so somehow the lone pairs must be involved in some process that stabilizes the alpha form. Turns out, the axial lone pair is the key here: it interacts with the sigma* antibonding orbital of the C-O bond on the anomeric carbon. By donating some of its electron density into the antibonding orbital, the bond between the ring oxygen and the anomeric carbon is strengthened, giving it some partial double bond character (Figure 8). It is for this reason that the alpha form is favoured. This is yet another example of NGP.
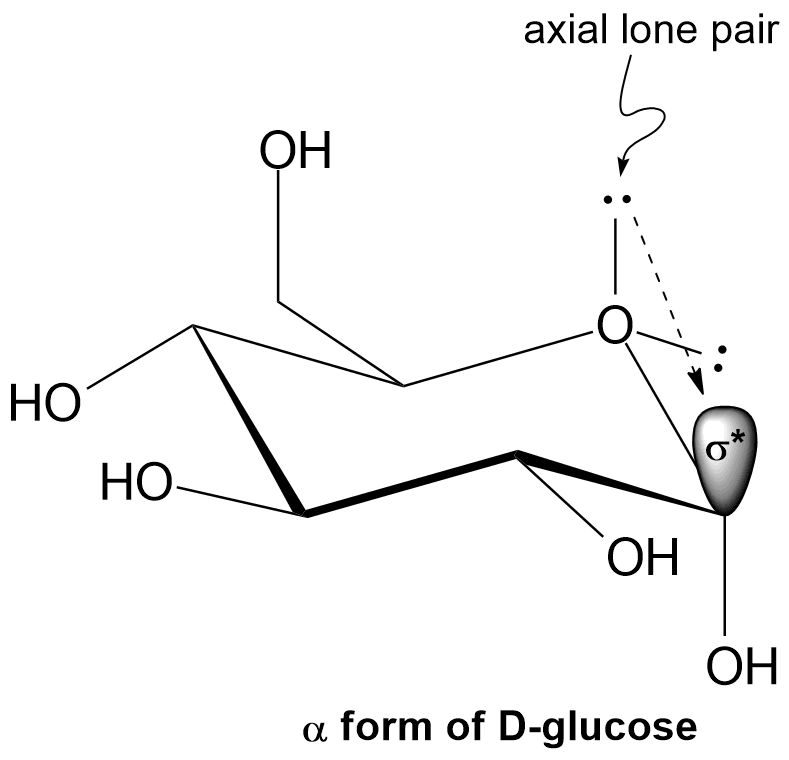
Any substituent on the anomeric carbon would be favoured towards the alpha form because of this anomeric effect.
Hopefully this article will serve as a useful short tutorial, and a reminder of sorts to always look out for and consider differences between compounds, especially in compare and contrast-type questions in exams.



Comments